A Fantástica sequência de Fibonacci
A proporção áurea está em tudo!
Na natureza,
na vida e em você.

A proporção áurea está em tudo!
Na natureza,
na vida e em você.
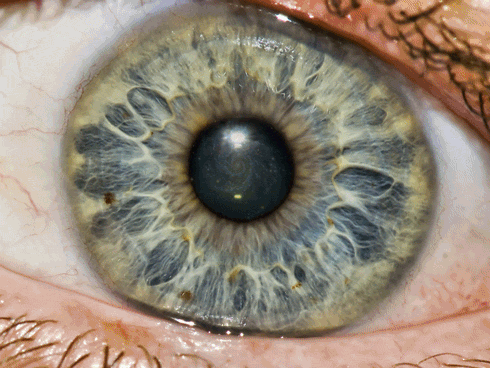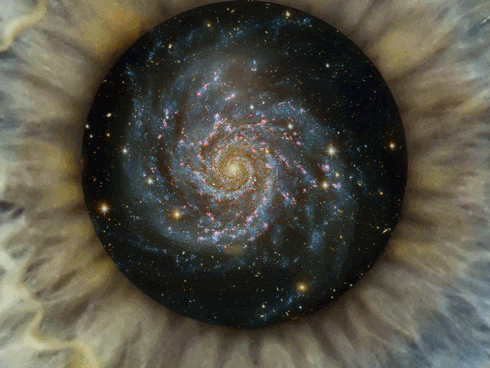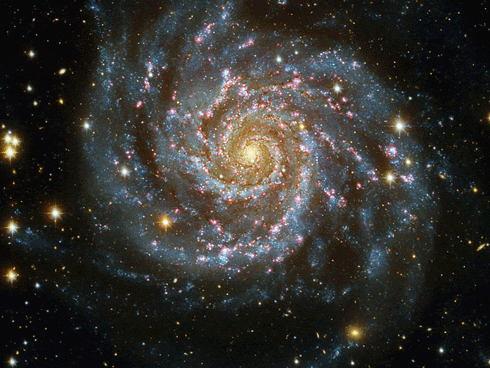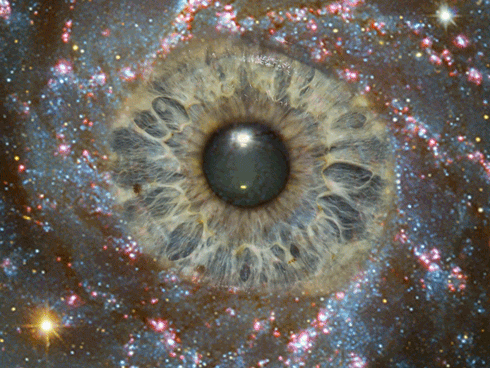
Os Antigos " sabiam muito mais do que dado o crédito a respeito de vida,universo ,
Astronomia, Matemática Avançada , Magnetismo , Cura , Forças Invisíveis etc
Conhecimento codificado é a informação que é transmitida em sinais e símbolos
e podemos encontrar esse conhecimento em todo o mundo .
Todos estes avistamentos antigos e padrões geométricos
simbolizam forças invisíveis no trabalho hoje.
A proporção Aurea(sequencia de Fibonacci)
está na formação da natureza,fauna,flora,animais e humanidade.
Deixando evidenciada uma inteligencia superior
aplicando tal conhecimento em sua criação e
permitindo a raça humana que
venha a conhecer uma parte de tal sabedoria.
Há muitos exemplos da Proporção Divina
encontrada em toda a concepção do universo
e em tudo que nele existe

Leonardo Fibonacci
A relação dourada é uma lei universal em que está contido o princípio base de todo formativa se esforçando para a beleza e a integralidade nos reinos da natureza e da arte, e que permeia, como um ideal espiritual primordial, todas as estruturas, formas e proporções , seja cósmico ou individual, orgânico ou inorgânico, sonoro ou visual; que tem a sua realização mais ampla, no entanto, sob a forma humana fica evidente.
Leonardo Pisano ou Leonardo de Pisa, nasceu nesta cidade italiana em 1170 e morreu em 1250. Foi o responsável, no começo do século XIII pela introdução da Aritmética e da Álgebra árabes no Ocidente. É considerado por alguns como o mais talentoso matemático da Idade Média. Ficou conhecido pela descoberta da sequência de Fibonacci. O apelido de família de seu pai foi "Bonacci" (homem de boa natureza) e ele mesmo, Fibonacci, que é o diminutivo de fillius Bonacci, que provavelmente seria filho de Bonacci. O pai dirigia um escritório comercial no norte da África e o jovem Leonardo muitas vezes viajou com ele. Lá, conheceu o sistema de numeração hindu. Fibonacci convenceu-se da superioridade dos algarismos árabes em comparação com os algarismos romanos, que eram utilizados pelos europeus à época. Viajou através dos países mediterrâneos para estudar junto de conhecidos matemáticos árabes de seu tempo. Em 1202, publicou Liber Abaci, Livro do Ábaco, que chegou a nós graças à sua segunda edição de 1228 . Este livro contém uma grande quantidade de assuntos relacionados com a Aritmética e Álgebra da época e realizou um papel importante no desenvolvimento matemático na Europa nos séculos seguintes pois foi por este livro que os europeus vieram a conhecer os algarismos hindus, também denominados árabes. A teoria contida no livro Liber Abacci é ilustrada com muitos problemas que representam uma grande parte do livro. Esclareceu o sistema de posição árabe dos números, inclusive o número zero. Este livro mostrou a oportunidade prática do novo sistema numeral, aplicando-o em contabilidade comercial, conversão de pesos e medidas, cálculo de percentagens e câmbio. O livro foi aceite com entusiasmo pela Europa educada e teve profundo efeito no pensamento europeu. Este elegante sistema de sinais numéricos, em breve, substituiu o não mais oportuno sistema de algarismos romanos.

A sequência de Fibonacci consiste numa sequência de números, tais que, definindo os dois primeiros números da sequência como sendo 0 e 1, os números seguintes são obtidos através da soma dos seus dois antecessores. Portanto, os números são: 0,1,1,2,3,5,8,13,21,34,55,89,144,233,... Dessa sequência se extrai o número transcendental conhecido como número de ouro. Recentemente a sequência de Fibonacci tornou-se um tema célebre da cultura popular ao ser citada no livro e filme O Código Da Vinci de Dan Brown.
A história do enigmático número de ouro perde-se na antiguidade. No Egipto, as Pirâmides de Gizé foram construídas tendo em conta a razão áurea : A razão entre a altura de um face e metade do lado da base da grande pirâmide é igual ao número de ouro. O Papiro de Rhind (Egípcio) refere-se a uma «razão sagrada» que se crê ser o número de ouro. Construído muitas centenas de anos depois( entre 447 e 433 a. C.) , o Partenon na Acrópole de Atenas , templo representativo do século de Péricles contém a razão de Ouro no rectângulo que contém a fachada (Largura / Altura), o que revela a preocupação de realizar uma obra bela e harmoniosa. O escultor e arquitecto encarregado da construção deste templo foi Fídias. A designação adoptada para o número de ouro é a inicial do nome deste arquitecto - a letra grega f (Phi maiúsculo). Os Pitagóricos usaram também a secção de ouro na construção da estrela pentagonal.
A espiral de Fibonacci
.jpg)
O que mais inspirou as gerações posteriores de matemáticos foi esse intrigante problema:
“Quantos pares (um macho e uma fêmea) de coelhos serão produzidos em um ano, começando com um único par, se em cada mês cada par gera um novo par que se torna fértil a partir do segundo mês?”
Este célebre problema dá origem à seqüência que leva o nome de Fibonacci:
Observe que cada termo, após os dois primeiros, é a soma dos dois imediatamente precedentes. Com um pouco de esforço qualquer pessoa medianamente treinada poderá criar outras seqüências desse tipo. Mas o que certamente nenhum leigo conseguirá - e é isso que torna a seqüência de Fibonacci deveras interessante - é a freqüência e a variedade de suas aparições na natureza e nas artes.Veja esses exemplos: o número de pequenas flores que formam o miolo do girassol é um dos números da seqüência de Fibonacci; o número de escamas de certos peixes e o número de segmentos da superfície de uma pinha são números da seqüência de Fibonacci; pode-se verificar que Virgílio e outros poetas romanos escreveram poemas nos quais a métrica está definida conforme as regras da seqüência de Fibonacci. [...] Outras investigações no campo da Botânica têm mostrado que as frações que representam a disposição espiral das folhas nos ramos são, com freqüência, membros da seqüência de Fibonacci.
É uma sucessão de números que, misteriosamente, aparece em muitos fenômenos da natureza. Descrita no final do século 12 pelo italiano Leonardo Fibonacci, ela é infinita e começa com 0 e 1. Os números seguintes são sempre a soma dos dois números anteriores. Portanto, depois de 0 e 1, vêm 1, 2, 3, 5, 8, 13, 21, 34…

Nautilus
Na espiral do nautilus, por exemplo, pode ser facilmente percebida a sequência de Fibonacci. A composição de quadrados com lados de medidas proporcionais aos números da sequência mostram a existência desta sucessão numérica nesta peça natural.
O primeiro quadrado terá os lados com medida 1, o segundo também, o terceiro terá os seus lados com medida 2, o quarto com medida 3, o quinto com medida 5, o sexto com medida 8 e, assim, sucessivamente.
Ao transformar esses números em quadrados e dispô-los de maneira geométrica, é possível traçar uma espiral perfeita, que também aparece em diversos organismos vivos. Outra curiosidade é que os termos da sequência também estabelecem a chamada “proporção áurea”, muito usada na arte, na arquitetura e no design por ser considerada agradável aos olhos. Seu valor é de 1,618 e, quanto mais você avança na sequência de Fibonacci, mais a divisão entre um termo e seu antecessor se aproxima desse número.

A espiral
Na espiral formada pela folha de uma bromélia, pode ser percebida a sequência de Fibonacci, através da composição de quadrados com arestas de medidas proporcionais aos elementos da sequência, por exemplo: 1, 1, 2, 3, 5, 8, 13… , tendentes à razão áurea. Este mesmo tipo de espiral também pode ser percebida na concha do Nautilus marinho.
Arranjos nas folhas
Os arranjos das folhas de algumas plantas em torno do caule são números de Fibonacci. Com este arranjo, todas as folhas conseguem apanhar os raios solares uniformemente. Esta formação, em caso de chuva, também facilita o escoamento da água na plant
Exemplos em que a sequência ou espiral de Fibonacci aparece na natureza:
CONCHA DO CARAMUJO
Cada novo pedacinho tem a dimensão da somados dois antecessores.
GIRASSOL / PINHA
No girasol as suas sementes preenchem o miolo dispostas em dois conjuntos de espirais: geralmente, 21 no sentido horário e 34 no anti-horário. As sementes de pinha crescem e se organizam em duas espirais que lembram a de Fibonacci: oito irradiando no sentido horário e 13 no anti-horário.
CAMALEÃO
Contraído, seu rabo é uma das representações mais perfeitas da espiral de Fibonacci.
POEMA
O “número de ouro” está presente até na razão entre as estrofes maiores e menores da Ilíada, épico de Homero sobre os últimos dias da Guerra de Troia.
PARTENON
Os gregos já conheciam a proporção, embora não a fórmula para defini-la. A largura e a altura da fachada deste templo do século V a.C. estão na proporção de 1 para 1,618.
GRANDES PIRÂMIDES
Mais um mistério: cada bloco é 1,618 vezes maior que o bloco do nível imediatamente acima. Em algumas, as câmaras internas têm comprimento 1,618 vezes maior que sua largura.
ARTES
Esse recurso matemático também foi uma das principais marcas do Renascimento. A Mona Lisa, de Leonardo da Vinci, usa a razão na relação entre tronco e cabeça e entre elementos do rosto.
A BELEZA DESCRITA EM NÚMEROS
A “Proporção de ouro” aparece tanto em seres vivos quanto em criações humanas. Na matemática, a razão dourada é representada pela letra grega phi: φ.
ELEFANTE
Se suas presas de marfim crescessem sem parar, ao final do processo o formato seria o da espiral de Fibonacci.
OBJETOS DO COTIDIANO
Vários formatos de cartão de crédito já foram testados. O que se sagrou favorito do público têm laterais na razão de ouro. Fotos e jornais também costumam adotá-la.
ROSTO / CORPO / MÃOS
Dizem que, nas faces consideradas mais harmoniosas, a divisão da distância entre o centro dos lábios e o “terceiro olho” pela distância entre esse ponto e uma das pupilas bate no 1,618. Se um humano “mediano” dividir sua altura pela distância entre o umbigo e a cabeça, o resultado será algo em torno de 1,618. Nas mãos, com exceção do polegar, em todos os outros dedos as articulações se relacionam na razão áurea.
Os dedos de Fibonacci:
Olhe para a sua mão!
Consegue ver:
|  |
Pétalas nas flores:
Em algumas plantas o número de pétalas é um número de Fibonacci:
3 pétalas: lírio, açucena, íris, trandescância.
5 pétalas: botão de ouro, rosa selvagem, columbine, esporas, capuchinha.
8 pétalas: delphiniums, anémona.
13 pétalas: malmequer, cineraria, ragwort.
21 pétalas: áster, olhado preto, susana, chicória.
34 pétalas: tanchagem, píretro, dália.
55,89 pétalas: margaridas(várias), a família asteraceae.
Algumas destas flores têm mesmo este número preciso de pétalas, outras podem variar mas sempre com um número de pétalas, perto do de Fibonacci.
Proporção áurea 1,618 - 0,618, triângulo isóceles, espiral, pentagrama e ângulos.
video,trazendo informações sobre a dinâmica de organização dos objetos na natureza através da sequência de Fibonacci e do número Phi – 1,618. O resultado é hipnotizante:
Principais obras: Liber abbaci, Practica geometriae e Liber quadratorum
Os números de Fibonacci também são encontrados na árvore genealógica de abelhas . 
spiral galaxy

..
Trabalhos de Fibonacci, em teoria, o número foi quase totalmente ignorado e praticamente desconhecidos durante a Idade Média. Trezentos anos mais tarde, encontramos os mesmos resultados que aparecem na obra de Maurolico.
O retrato acima é de uma gravura moderna e acredita-se não estar baseado em fontes autênticas.
O retrato acima é de uma gravura moderna e acredita-se não estar baseado em fontes autênticas.
Razão Áurea na Natureza
matemática
proporção áurea expressa
proporção áurea expressa
no arranjo dos ramos ao longo das hastes das plantas e das veias nas folhas,
esqueletos de animais
e as ramificações de suas veias e nervos,
às proporções de compostos químicos e da geometria dos cristais,
até mesmo para o uso de proporção em empreendimentos artísticos.
Nesses fenômenos existem o funcionamento proporção áurea como uma lei universal
Onde há uma mudança na densidade, um vórtice espiral aparece, é por isso que tudo no universo em todas as escalas esta constantemente girando.
Em todas as escalas, o padrão matemático que gera este vórtice é o mesmo: Phi - 1:1.618 - the Golden Ratio e a espiral de Fibonacci
The Resonance Project The Resonance Project - Página Oficial HispanaThe Resonance Project - Traduction Française The connected universeJamie Janover Ciência e Meditação (por Flávio Morone)
Relações fundamentais da proporção entre a Terra e a Lua estão codificadas na Grande Pirâmide de Gizé como os números de Fibonacci, os número Pi e Phi, e até mesmo a velocidade da luz.
Nassim Haramein The Resonance Project The Resonance Project - Traduction Française The Resonance Project - Página Oficial HispanaJamie Janover (post or Flávio Morone)






Nenhum comentário:
Postar um comentário